Difference-in-Differences: What it DiD?
Andrew Baker
Stanford University
2020-05-25
Outline of Talk
\(\hspace{2cm}\)
Overview of DiD
Problems with Staggered DiD
Simulation Results
Some Alternative Methods
Application
Difference-in-Differences
\(\hspace{2cm}\)
Think Card and Krueger minimum wage study comparing NJ and PA.
2 units and 2 time periods.
1 unit (T) is treated, and receives treatment in the second period. The control unit (C) is never treated.
Difference-in-Differences
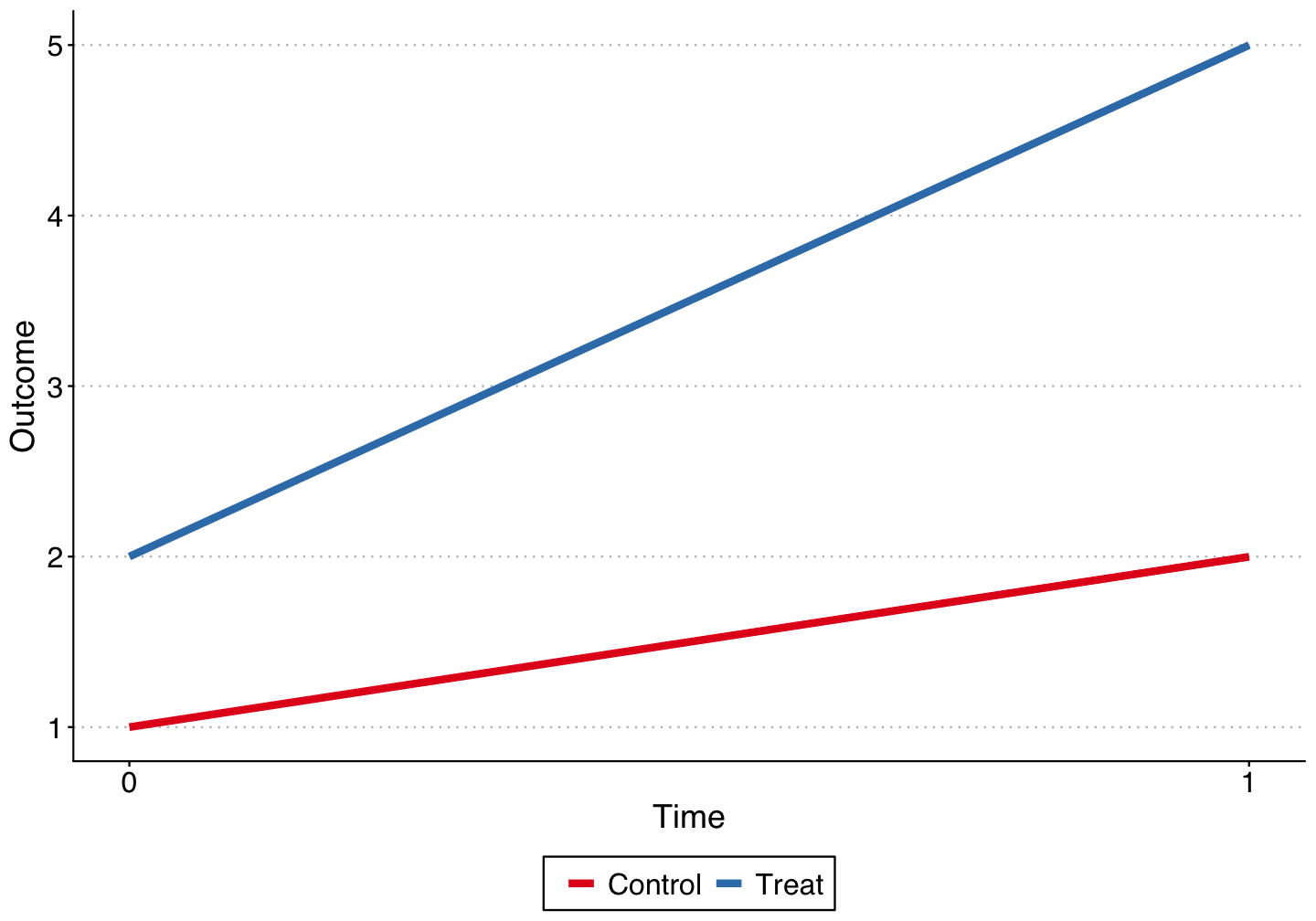
Difference-in-Differences
Building upon \(\color{blue}{\text{Angrist & Pischke (2008, p. 228)}}\) we can think of these simple 2x2 DiDs as a fixed effects estimator.
Potential Outcomes
- \(Y_{i, t}^1\) = value of dependent variable for unit \(i\) in period \(t\) with treatment.
- \(Y_{i, t}^0\) = value of dependent variable for unit \(i\) in period \(t\) without treatment.
The expected outcome is a linear function of unit and time fixed effects: $$E[{Y_{i, t}^0}] =\alpha_i + \alpha_t$$ $$E[{Y_{i, t}^1}] =\alpha_i + \alpha_t + \delta D_{st}$$
- Goal of DiD is to get an unbiased estimate of the treatment effect \(\delta\).
Difference-in-Differences as Solving System of Equations for Unknown Variable
Difference in expectations for the control unit times t = 1 and t = 0: $$\begin{align*} E[Y_{C, 1}^0] & = \alpha_1 + \alpha_C \\ E[Y_{C, 0}^0] & = \alpha_0 + \alpha_C \\ E[Y_{C, 1}^0] - E[Y_{C, 0}^0] & = \alpha_1 - \alpha_0 \end{align*}$$
Now do the same thing for the treated unit: $$\begin{align*} E[Y_{T, 1}^1] & = \alpha_1 + \alpha_T + \delta \\ E[Y_{T, 0}^1] & = \alpha_0 + \alpha_T \\ E[Y_{T, 1}^1] - E[Y_{T, 0}^1] & = \alpha_1 - \alpha_0 + \delta \end{align*}$$
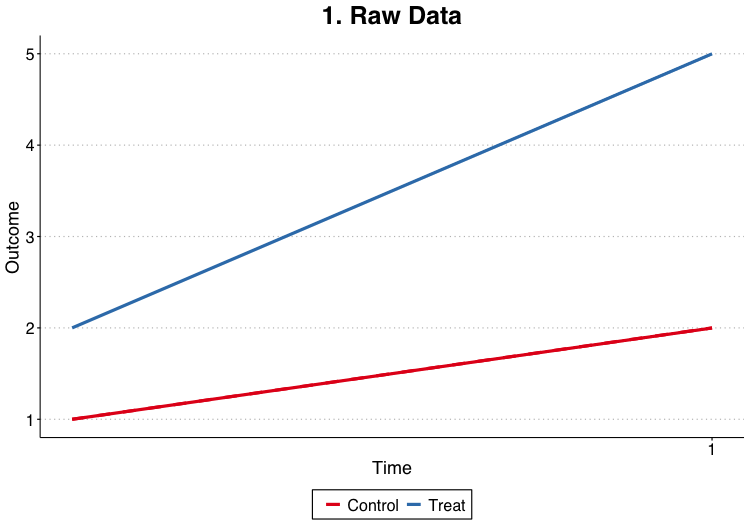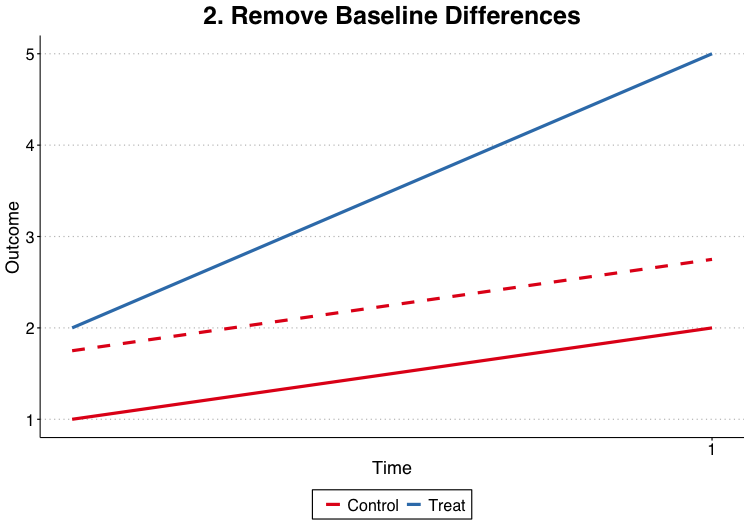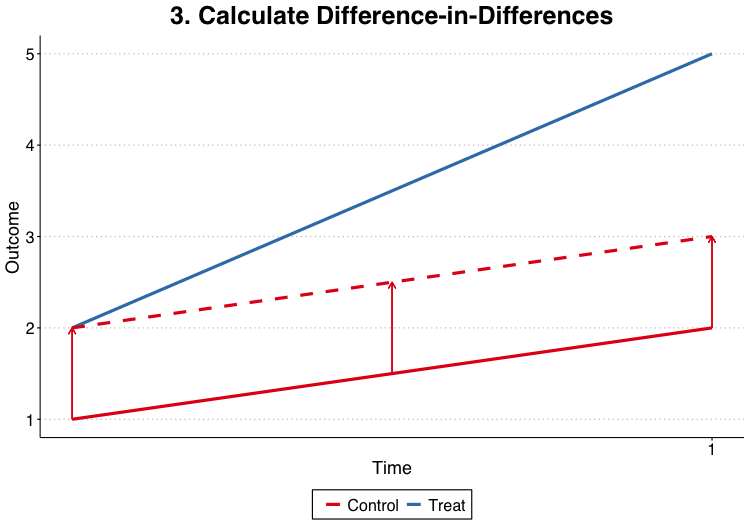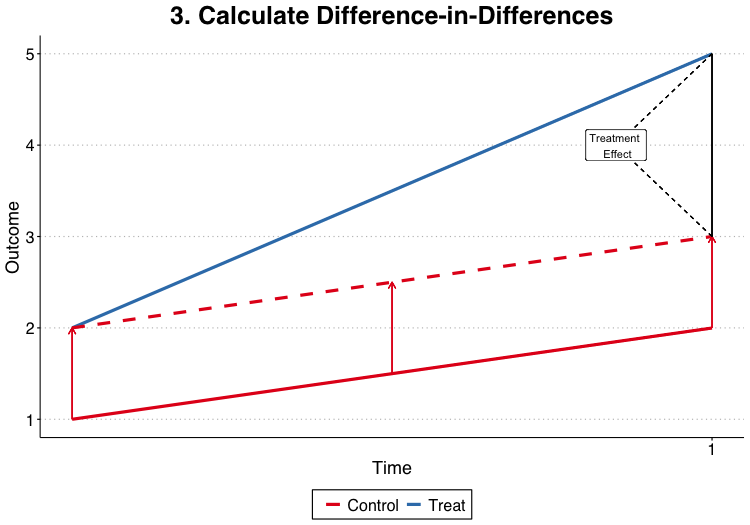
- If we assume the linear structure of DiD, then unbiased estimate of \(\delta\) is:
$$\delta= \begin{align*} & \left( E[Y_{T, 1}^1] - E[Y_{T, 0}^1] \right) - \left( E[Y_{C, 1}^0] - E[Y_{C, 0}^0] \right) \end{align*}$$
Two-Way Differencing
Regression DiD
The DiD can be estimated through linear regression of the form:
$$\tag{1} y_{it} = \alpha + \beta_1 TREAT_i + \beta_2 POST_t + \delta (TREAT_i \cdot POST_t) + \epsilon_{it}$$
The coefficients from the regression estimate in (1) recover the same parameters as the double-differencing performed above: $$\begin{align*} \alpha &= E[y_{it} | i = C, t = 0] = \alpha_0 + \alpha_C \\ \beta_1 &= E[y_{it} | i = T, t = 0] - E[y_{it} | i = C, t= 0] \\ &= (\alpha_0 + \alpha_T) - (\alpha_0 + \alpha_C) = \alpha_T - \alpha_C \\ \beta_2 &= E[y_{it} | i = C, t = 1] - E[y_{it} | i = C, t = 0] \\ &= (\alpha_1 + \alpha_C) - (\alpha_0 + \alpha_C) = \alpha_1 - \alpha_0 \\ \delta &= \left(E[y_{it} | i = T, t = 1] - E[y_{it} | i = T, t = 0] \right) - \\ &\hspace{.5cm} \left(E[y_{it} | i = C, t = 1] - E[y_{it} | i = C t = 0] \right) = \delta \end{align*}$$
Regression DiD

Regression DiD - The Workhorse Model
Advantage of regression DiD - it provides both estimates of \(\delta\) and standard errors for the estimates.
\(\color{blue}{\text{Angrist & Pischke (2008)}}\):
- "It's also easy to add additional (units) or periods to the regression setup... [and] it's easy to add additional covariates."
Two-way fixed effects estimator: $$y_{it} = \alpha_i + \alpha_t + \delta^{DD} D_{it} + \epsilon_{it}$$
\(\alpha_i\) and \(\alpha_t\) are unit and time fixed effects, \(D_{it}\) is the unit-time indicator for treatment.
\(TREAT_i\) and \(POST_t\) now subsumed by the fixed effects.
can be easily modified to include covariate matrix \(X_{it}\), time trends, dynamic treatment effects estimation, etc.
Where It Goes Wrong
Developed literature now on the issues with TWFE DiD with "staggered treatment timing" (Abraham and Sun (2018), Borusyak and Jaravel (2018), Callaway and Sant'Anna (2019), Goodman-Bacon (2019), Strezhnev (2018), Athey and Imbens (2018))
- Different units receive treatment at different periods in time.
Probably the most common use of DiD today. If done right can increase amount of cross-sectional variation.
Without digging into the literature:
\(\delta^{DD}\) with staggered treatment timing is a weighted average of many different treatment effects.
We know little about how it measures when treatment timing varies, how it compares means across groups, or why different specifications change estimates.
The weights are often negative and non-intuitive.
Bias with TWFE - Goodman-Bacon (2019)
- \(\color{blue}{\text{Goodman-Bacon (2019)}}\) provides a clear graphical intuition for the bias. Assume three treatment groups - never treated units (U), early treated units (k), and later treated units (l).
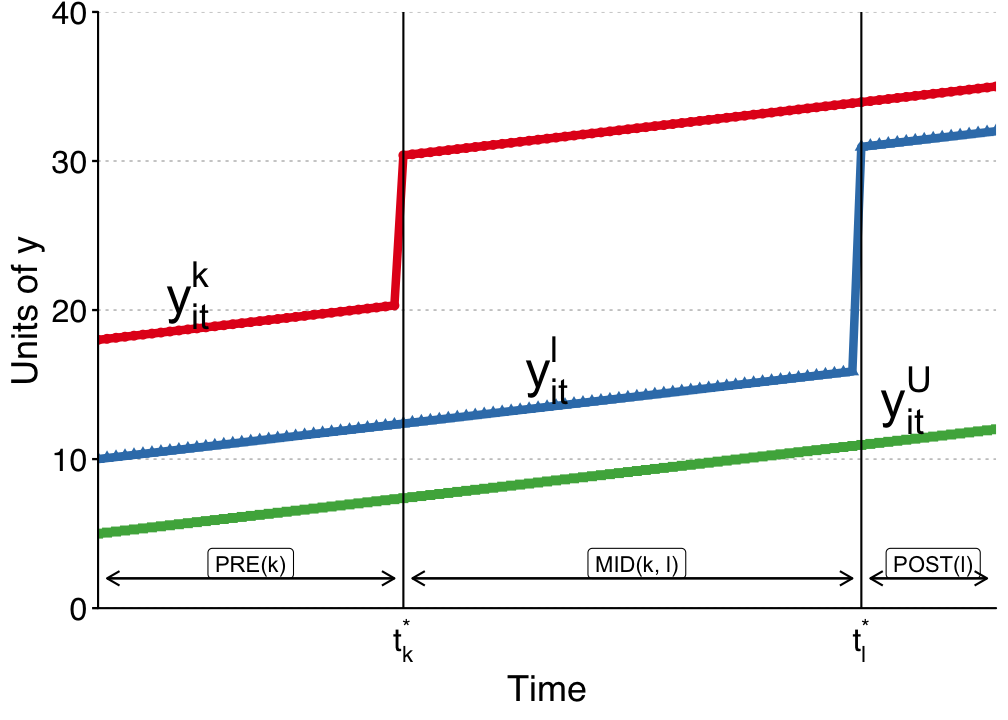
Bias with TWFE - Goodman-Bacon (2019)
- \(\color{blue}{\text{Goodman-Bacon (2019)}}\) shows that we can form four different 2x2 groups in this setting, where the effect can be estimated using the simple regression DiD in each group:
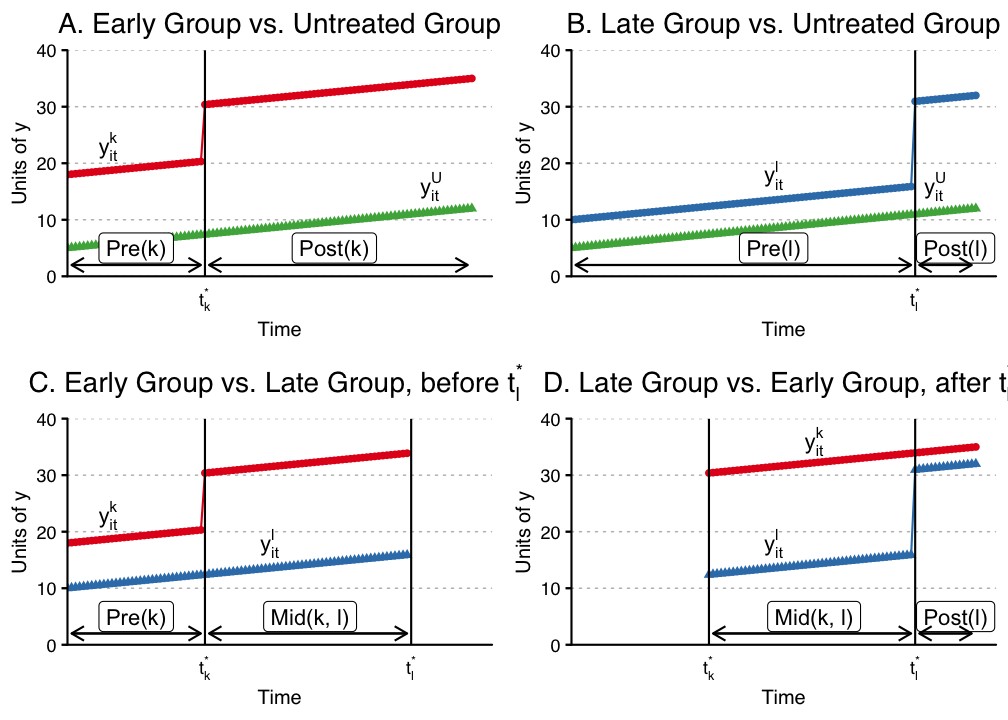
Bias with TWFE - Goodman-Bacon (2019)
Important Insights
\(\delta^{DD}\) is just the weighted average of the four 2x2 treatment effects. The weights are a function of the size of the subsample, relative size of treatment and control units, and the timing of treatment in the sub sample.
Already-treated units act as controls even though they are treated.
Given the weighting function, panel length alone can change the DiD estimates substantially, even when each \(\delta^{DD}\) does not change.
Groups treated closer to middle of panel receive higher weights than those treated earlier or later.
Simulation Exercise
Can show how easily \(\delta^{DD}\) goes awry up through a simulation exercise.
Consider two sets of DiD estimates - one where the treatment occurs in one period, and one where the treatment is staggered.
The data generating process is linear: \(y_{it} = \alpha_i + \alpha_t + \delta_{it} + \epsilon_{it}\).
- \(\alpha_i, \alpha_t \sim N(0, 1)\)
- \(\epsilon_{i, t} \sim N\left(0, \left(\frac{1}{2}\right)^2\right)\)
We will consider two different treatment assignment set ups for \(\delta_{it}\).
Simulation 1 - 1 Period Treatment
There are 40 states \(s\), and 1000 units \(i\) randomly drawn from the 40 states.
Data covers years 1980 to 2010, and half the states receive "treatment" in 1995.
For every unit incorporated in a treated state, we pull a unit-specific treatment effect from \(\mu_i \sim N(0.3, (1/5)^2)\).
Treatment effects here are trend breaks rather than unit shifts: the accumulated treatment effect \(\delta_{it}\) is \(\mu_i \times (year - 1995 + 1)\) for years after 1995.
We then estimate the average treatment effect as \(\hat{\delta}\) from:
$$y_{it} = \hat{\alpha_i} + \hat{\alpha_t} + \hat{\delta} D_{it}$$
Simulate this data 1,000 and plot the distribution of estimates \(\hat{\delta}\) and the true effect (red line).
Simulation 1 - 1 Period Treatment
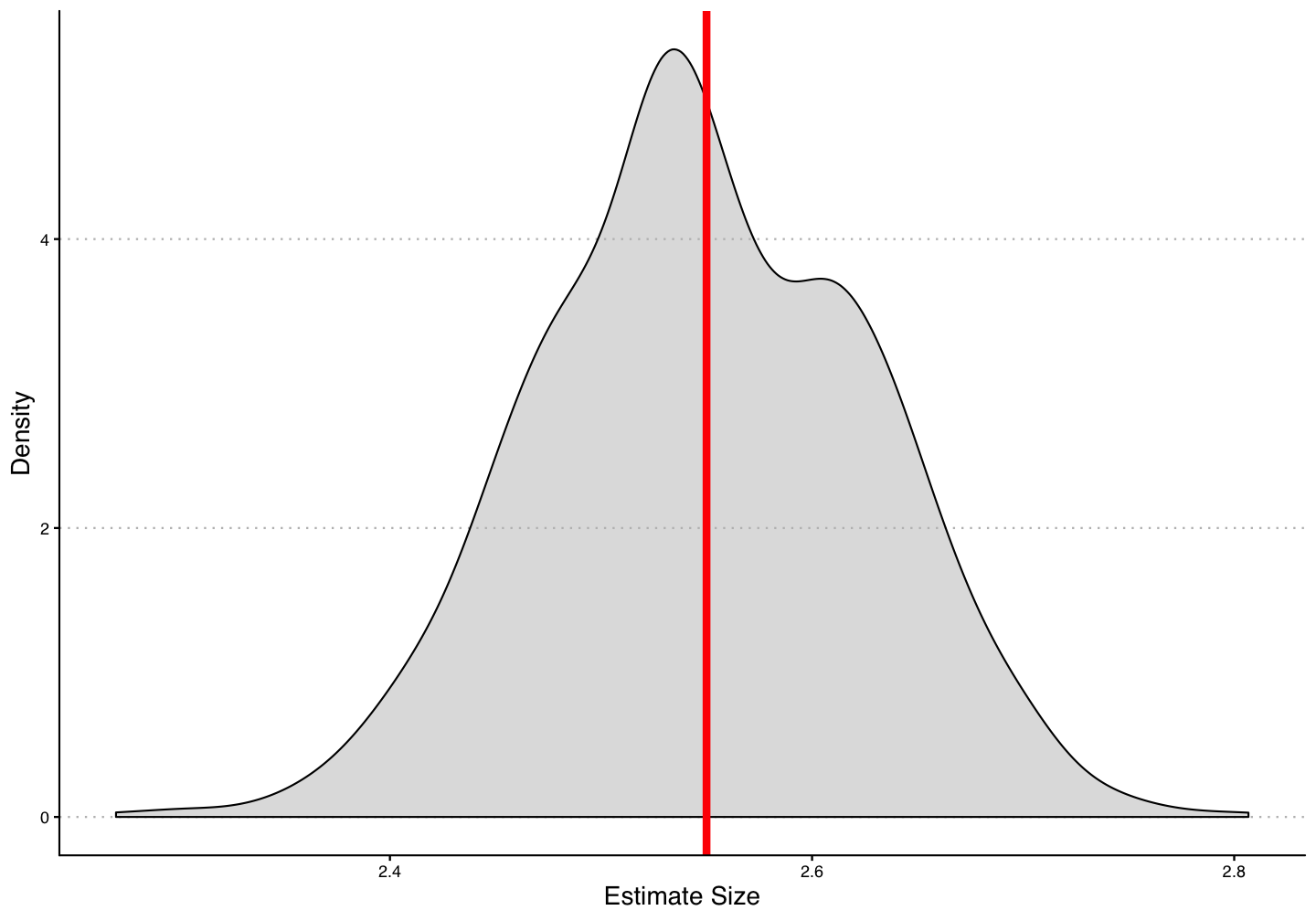
Simulation 1 - 1 Period Treatment

Simulation 2 - Staggered Treatment
Run similar analysis with staggered treatment.
The 40 states are randomly assigned into four treatment cohorts of size 250 depending on year of treatment assignment (1986, 1992, 1998, and 2004)
DGP is identical, except that now \(\delta_{it}\) is equal to \(\mu_i \times (year - \tau_g + 1)\) where \(\tau_g\) is the treatment assignment year.
Estimate the treatment effect using TWFE and compare to the analytically derived true \(\delta\) (red line).
Simulation 2 - Staggered Treatment
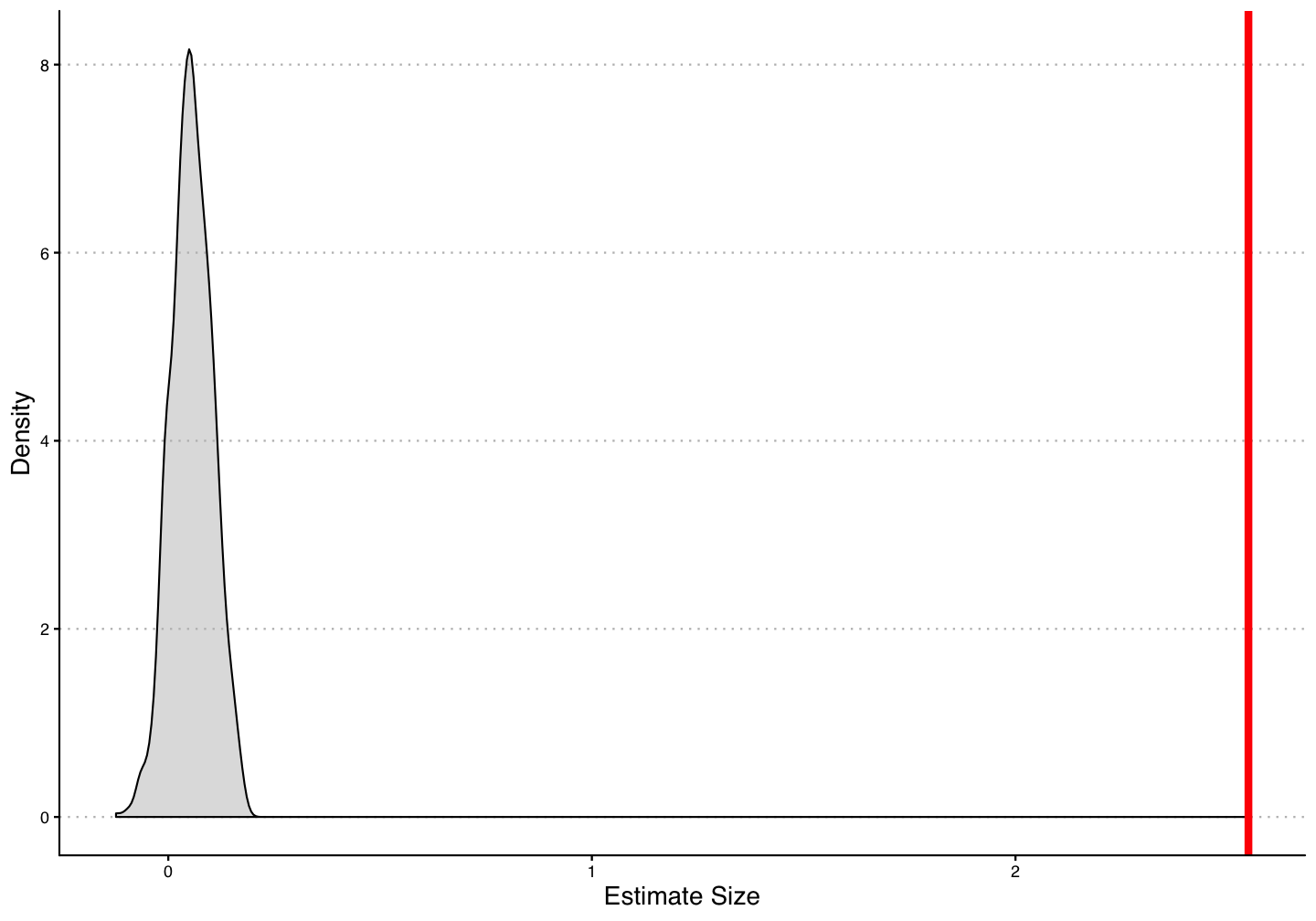
Simulation 2 - Staggered Treatment

Simulation 2 - Staggered Treatment
Main problem - we use prior treated units as controls.
When the treatment effect is "dynamic", i.e. takes more than one period to be incorporated into your dependent variable, you are subtracting the treatment effects from prior treated units from the estimate of future control units.
This biases your estimates towards zero when all the treatment effects are the same.
Another Simulation
Can we actually get estimates for \(\delta\) that are of the wrong sign? Yes, if treatment effects for early treated units are larger (in absolute magnitude) than the treatment effects on later treated units.
Here firms are randomly assigned to one of 50 states. The 50 states are randomly assigned into one of 5 treatment groups \(G_g\) based on treatment being initiated in 1985, 1991, 1997, 2003, and 2009.
All treated firms incorporated in a state in treatment group \(G_g\) receive a treatment effect \(\delta_i \sim N(\delta_g, .2^2)\).
The treatment effect is cumulative or dynamic - \(\delta_{it} = \delta_i \times (year - G_g)\).
Another Simulation
- The average treatment effect multiple decreases over time:
\(\hspace{2cm}\)
| `\(G_g\)` | `\(\delta_g\)` |
|---|---|
| 1985 | 0.5 |
| 1991 | 0.4 |
| 1997 | 0.3 |
| 2003 | 0.2 |
| 2009 | 0.1 |
Another Simulation
- First let's look at the distribution of \(\delta^{DD}\) using TWFE estimation with this simulated sample:
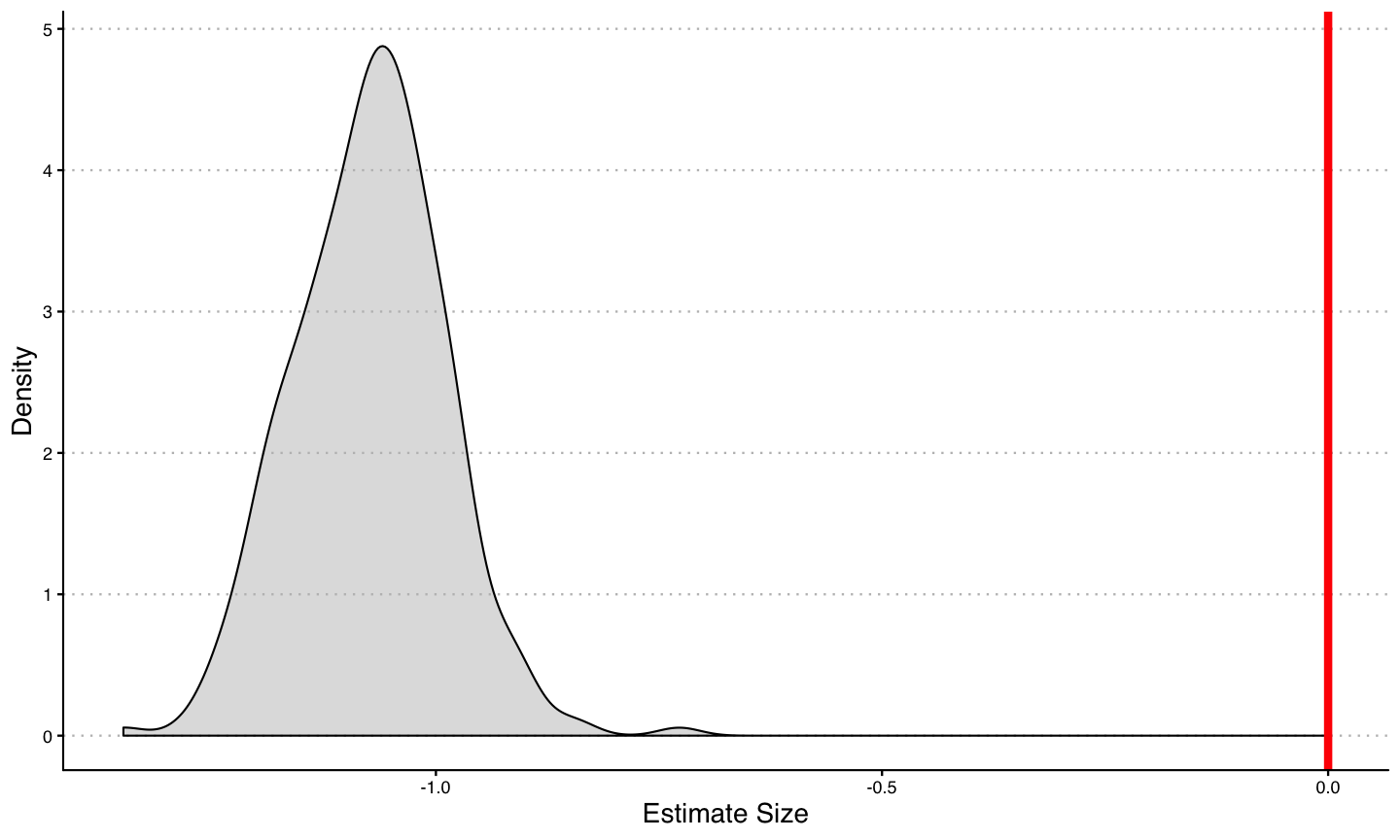
Goodman-Bacon Decomposition
Callaway & Sant'Anna
- Inverse propensity weighted long-difference in cohort-specific average treatment effects between treated and untreated units for a given treatment cohort.
$$\begin{equation} ATT(g, t) = \mathbb{E} \left[\left( \frac{G_g}{\mathbb{E}[G_g]} - \frac{\frac{p_g(X)C}{1 - p_g(X)}}{\mathbb{E}\left[\frac{p_g(X)C}{1 - p_g(X)} \right]} \right) \left(Y_t - T_{g - 1}\right)\right] \end{equation}$$
- Without covariates, as in the simulated example here, it calculates the simple long difference between all treated units \(i\) in relative year \(k\) with all potential control units that have not yet been treated by year \(k\).
Callaway & Sant'Anna
Abraham and Sun
A relatively straightforward extension of the standard event-study TWFE model:
$$y_{it} = \alpha_i + \alpha_t + \sum_e \sum_{l \neq -1} \delta_{el}(1\{E_i = e\} \cdot D_{it}^l) + \epsilon_{it}$$
You saturate the relative time indicators (i.e. t = -2, -1, ...) with indicators for the treatment initiation year group, and aggregate to overall aggregate relative time indicators by cohort size.
In the case of no covariates, this gives you the same estimate as Callaway & Sant'Anna if you fully saturate the model with time indicators (leaving only two relative year identifiers missing).
The authors don't claim that it can be used with covariates, but it seemingly follows if we think it is okay with normal TWFE DiD.
Abraham and Sun
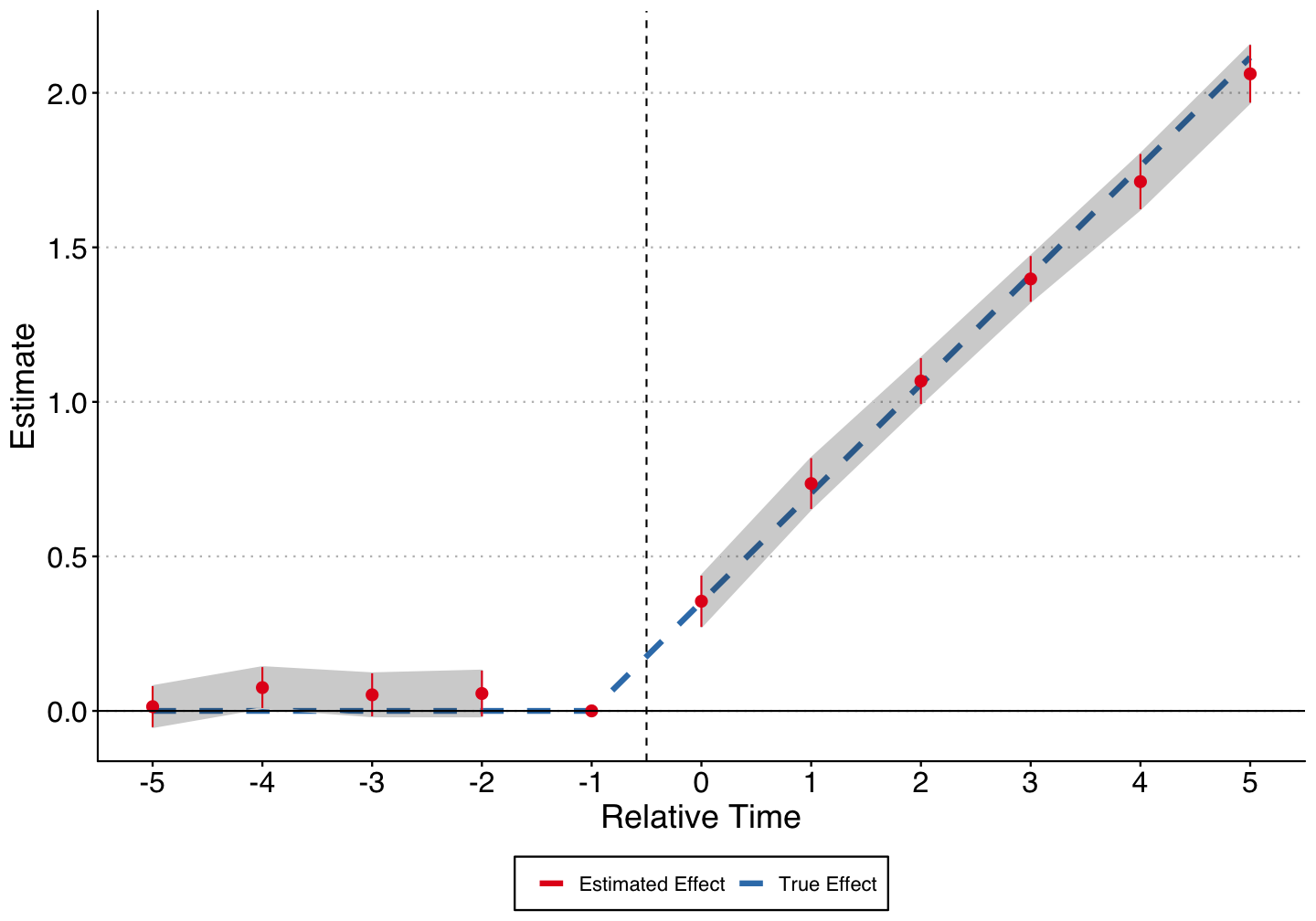
Cengiz et al. (2019)
Similar to the standard TWFE DiD, but we ensure that no previously treated units enter as controls by trimming the sample.
For each treatment cohort \(G_g\), get all treated units, and all units that are not treated by year \(g + k\) where \(g\) is the treatment year and \(k\) is the outer most relative year that you want to test (e.g. if you do an event study plot from -5 to 5, \(k\) would equal 5).
Keep only observations within years \(g - k\) and \(g + k\) for each cohort-specific dataset, and then stack them in relative time.
Run the same TWFE estimates as in standard DiD, but include interactions for the cohort-specific dataset with all of the fixed effects, controls, and clusters.
Cengiz et al. (2019)
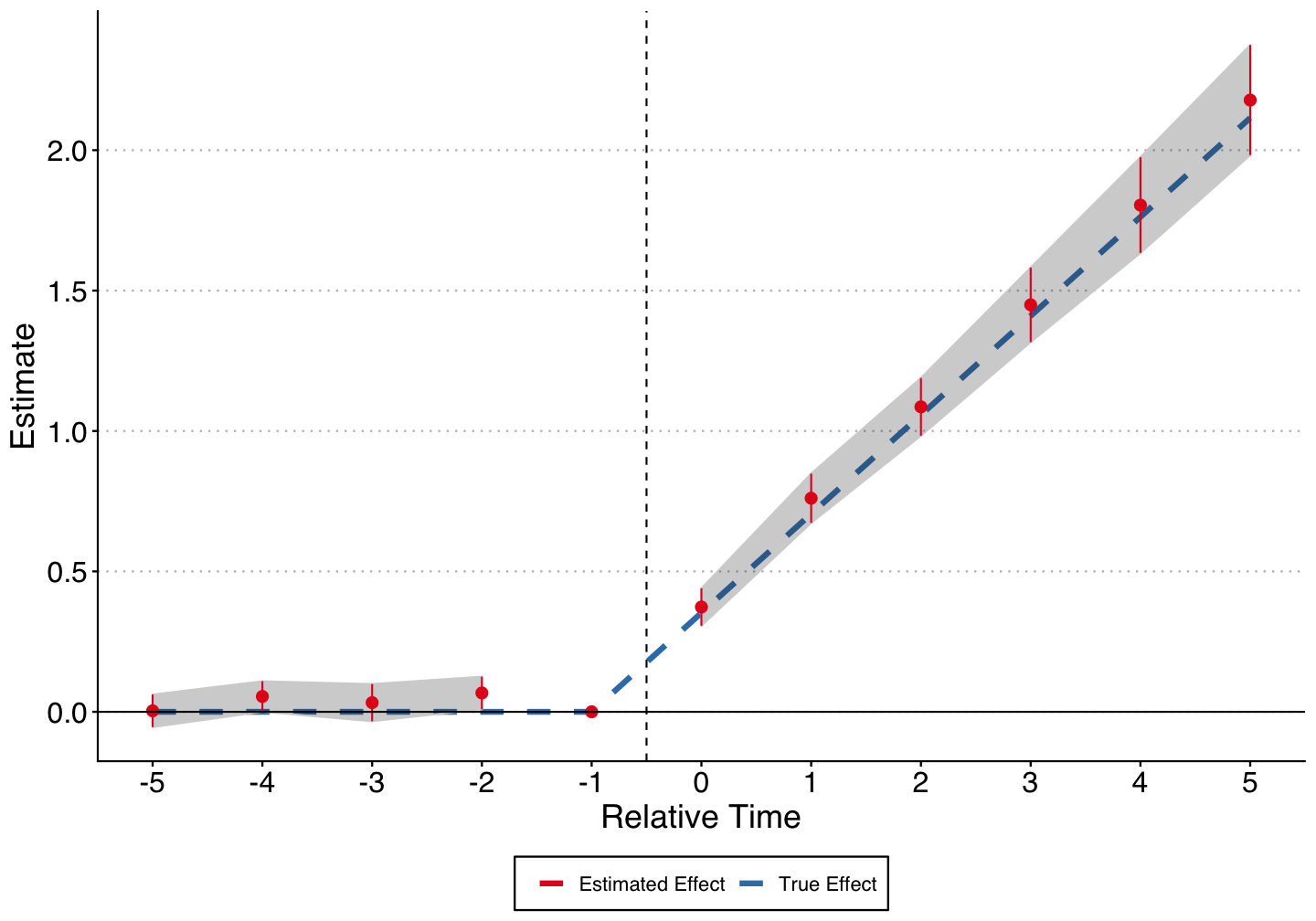
Model Comparison
In the stylized example all the models work. How do they differ?
Callaway & Sant'Anna
- Can be very flexible in determining which control units to consider.
- Has a more flexible functional form as well (IPW instead of OLS).
- IPW can run into issues with p-scores near 0 or 1. But just bc OLS runs doesn't mean it's right!
Abraham & Sun
- Very similar to regular TWFE OLS and hence easy to explain.
- Control units are all units not treated within the data sample. If most of your units are treated by the end (or all), this can make control units very non-representative and restricted.
Cengiz et al.
- Also fairly close to regular DiD.
- Can modify this framework to allow different forms of control units as well.
- Not theoretically derived.
Application - Medical Marijuana Laws and Opioid Overdose Deaths
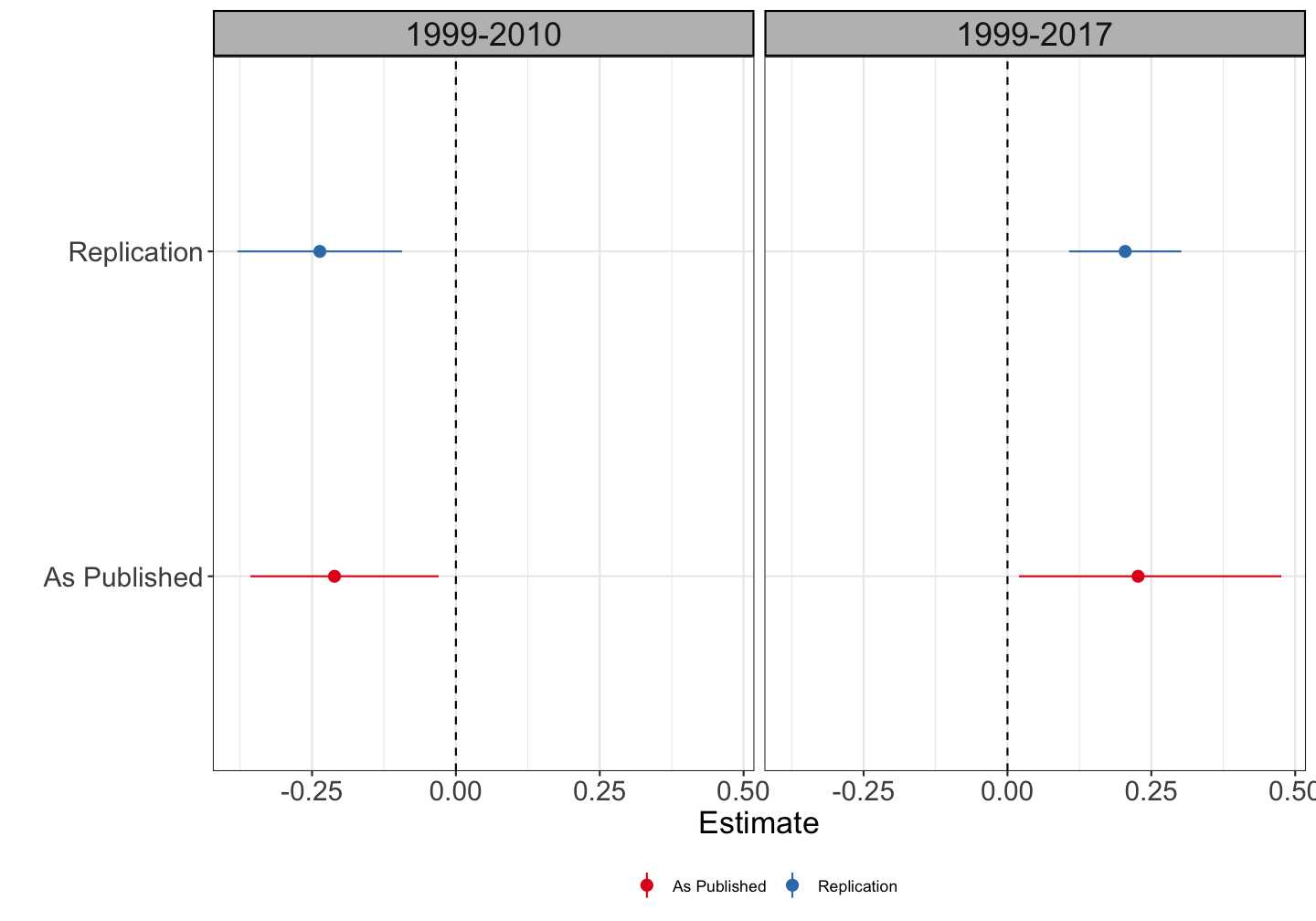
\(\color{blue}{\text{Bachhuber et al. 2014}}\) found, using a staggered DiD, that states with medical cannabis laws experienced a slower increase in opioid overdose mortality from 1999-2010.
\(\color{blue}{\text{Shover et al. 2020}}\) extend the data sample from 2010 to 2017, a period during which 32 extra states passed MML laws.
Not only do the results go away, but the sign flips; MML laws are associated with higher opioid overdose mortality rates.
Authors don't call it difference-in-differences, but it uses TWFE with a binary indicator variable (thus is effectively DiD).
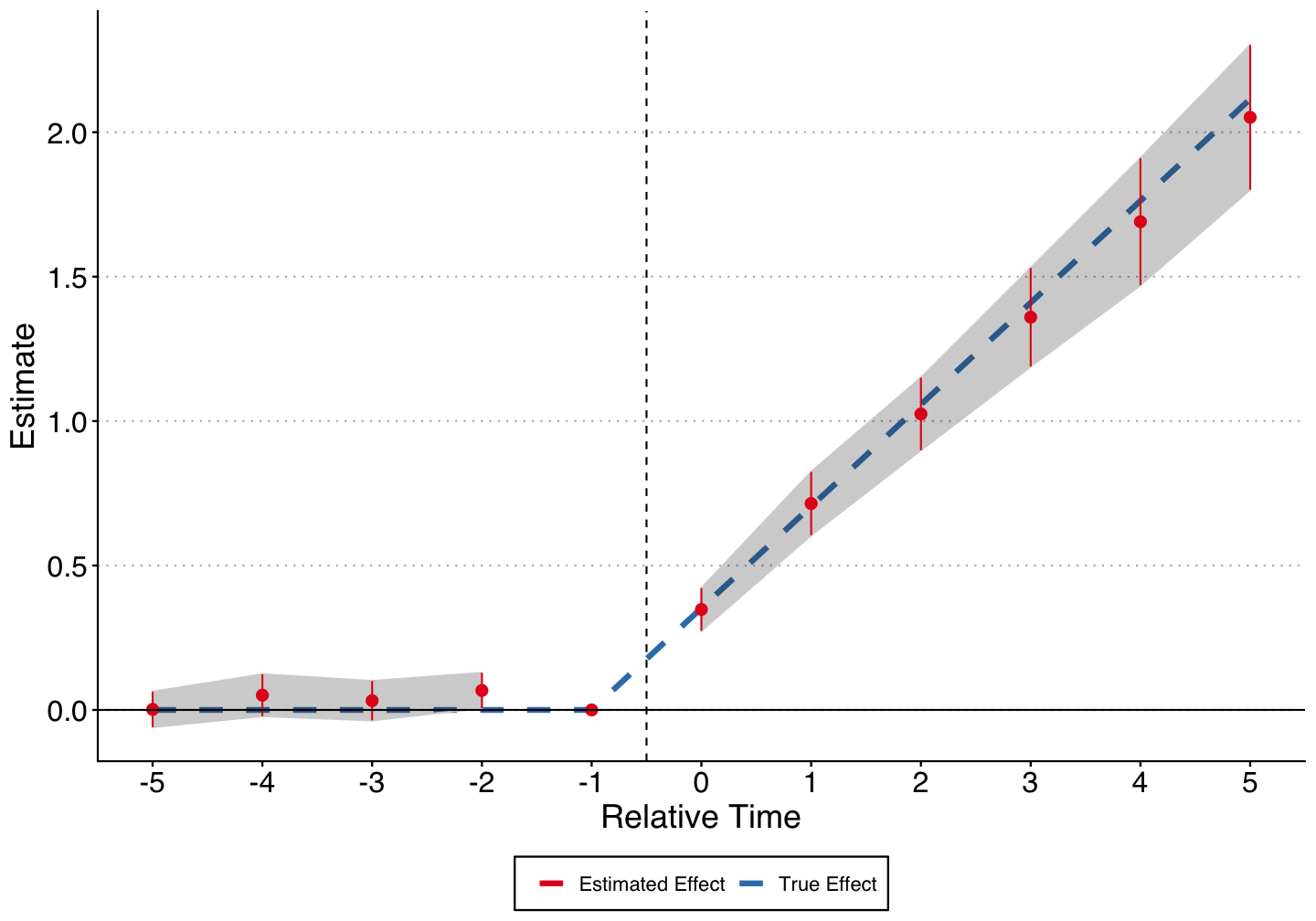
Replication
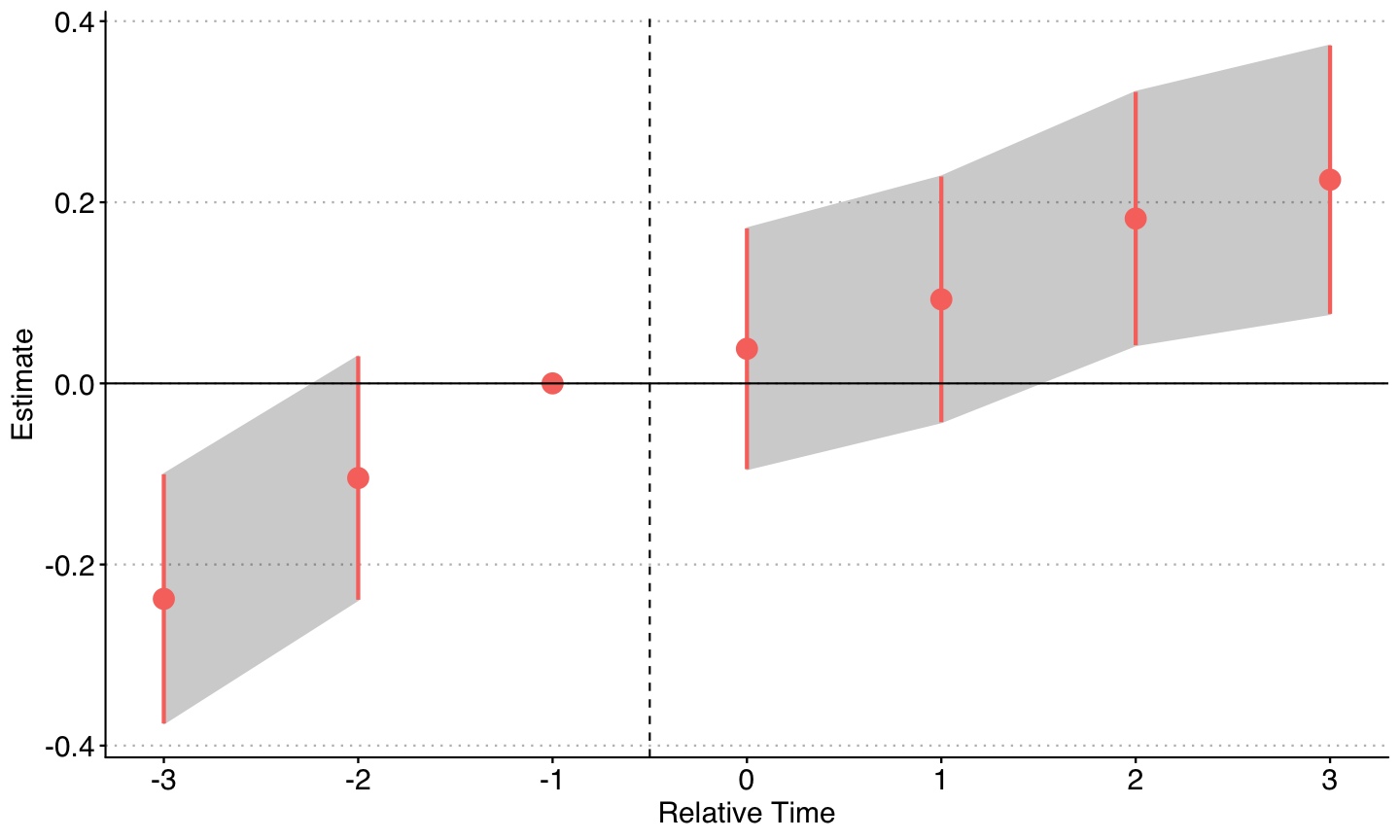
Event Study Estimates
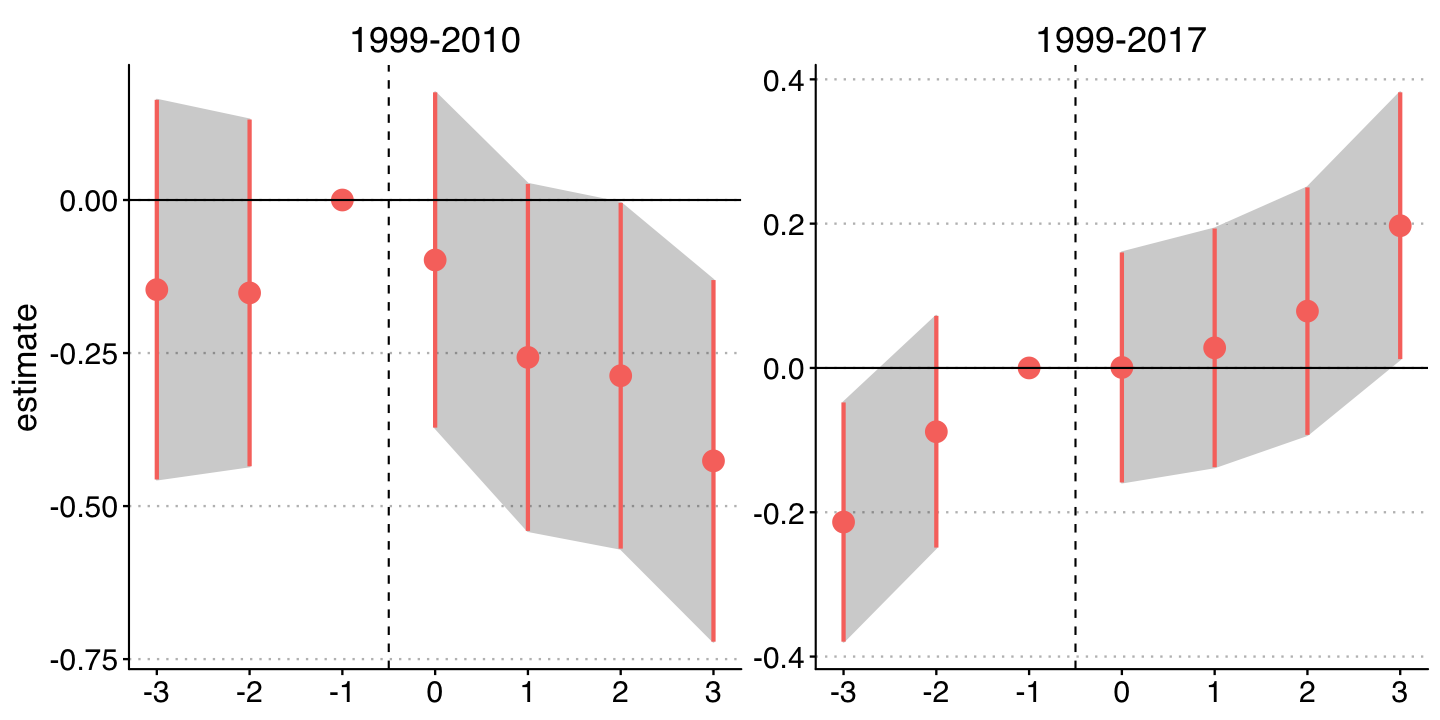
Little evidence covariates matter here, so estimate standard DiD with no controls over the two periods:
$$y_{it} = \alpha_i + \alpha_t + \sum_{k = Pre, Post} \delta_k + \sum_{-3}^3 \delta_k + \epsilon_{it}$$
Event Study Estimates
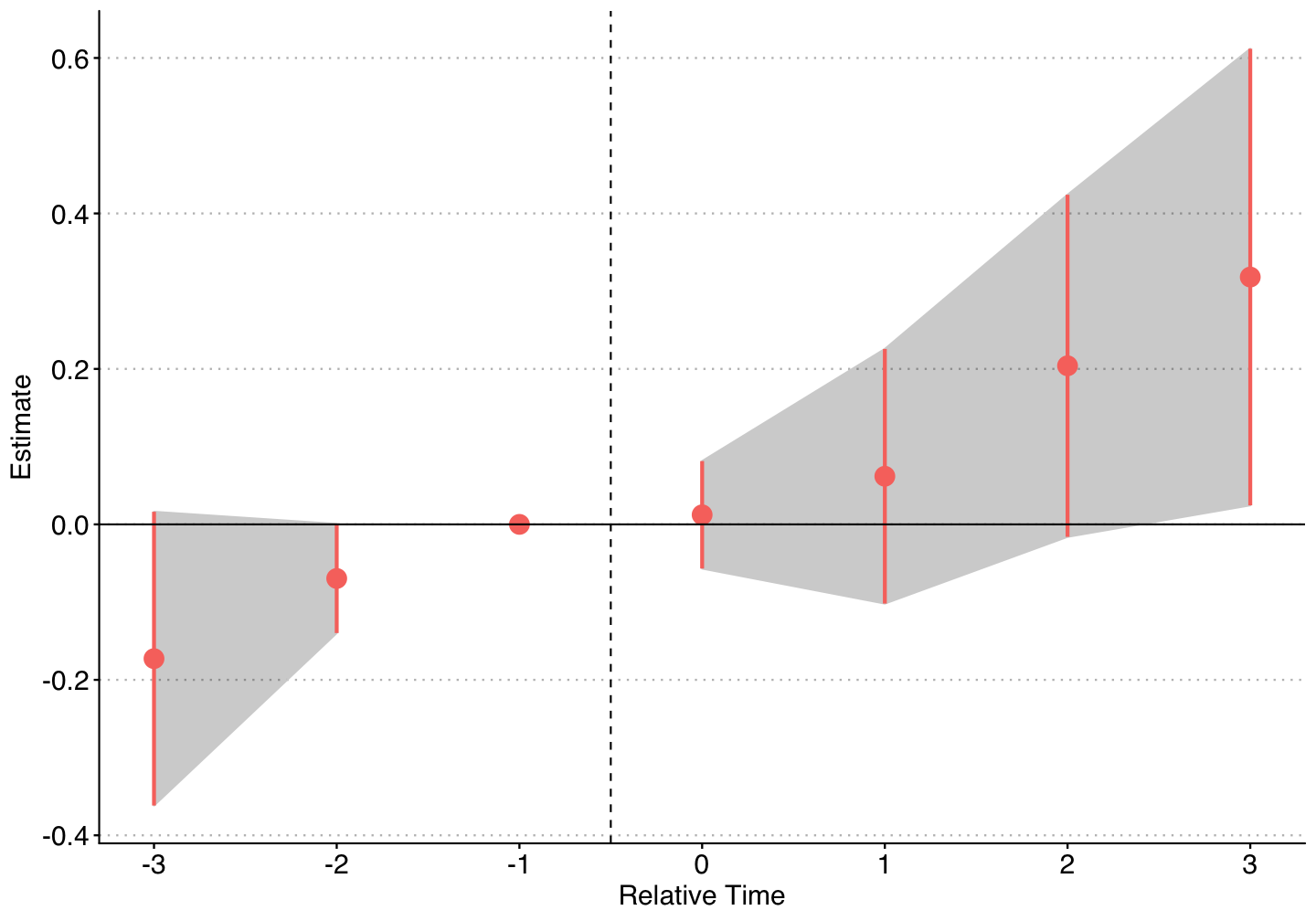
So we can verify that in the first sample (1999 - 2010), there appears to be a negative effect of law introduction, while in the full sample (1999 - 2017), there is a positive effect.
But there appears to be evidence of pre-trends in the full sample.
In addition, by the end of the sample the number of firms adopting MMLs is quite large.
If there are dynamic treatment effects, then these estimates could be biased from using many prior treated states as controls.
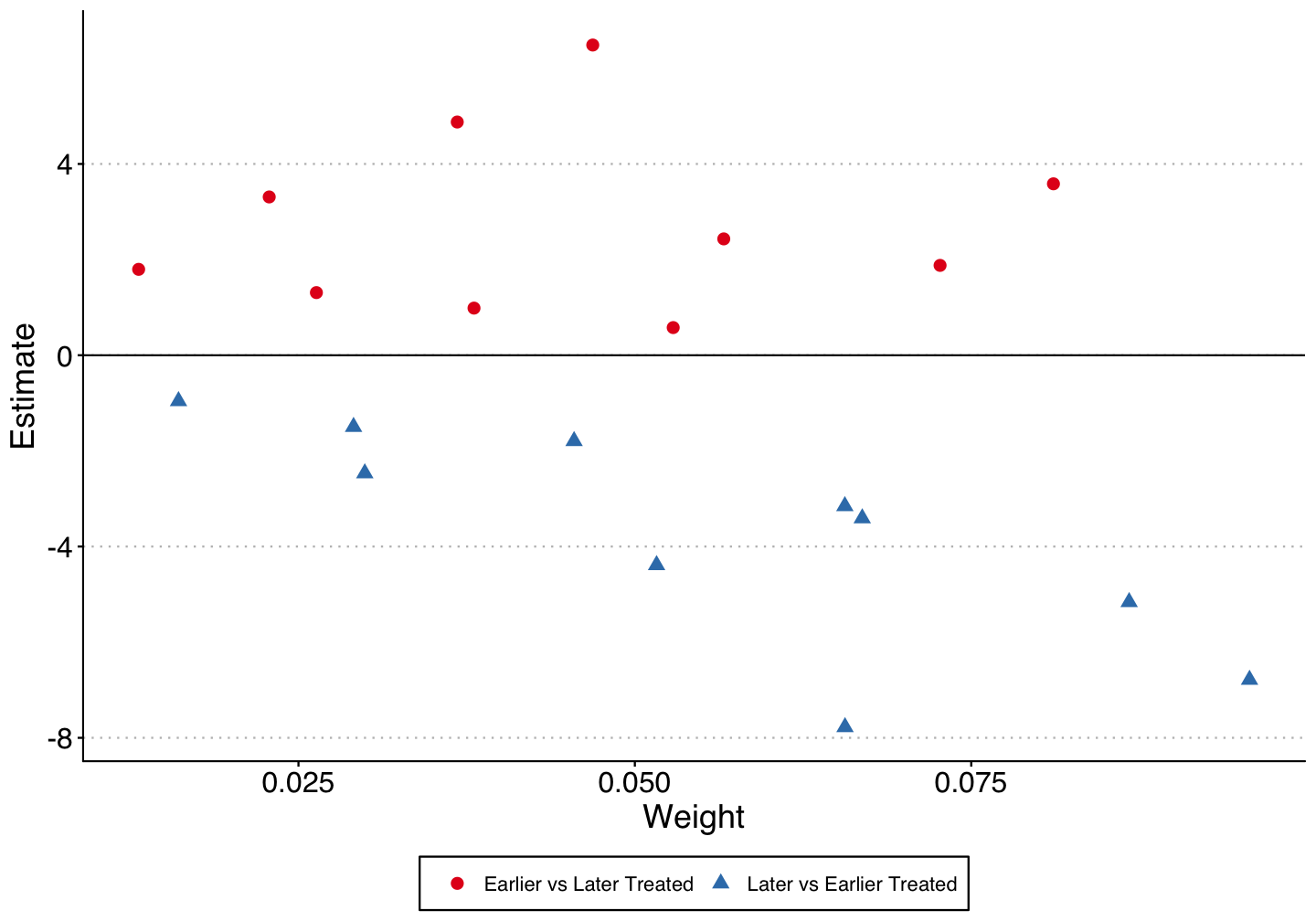
Bacon-Goodman Decomposition
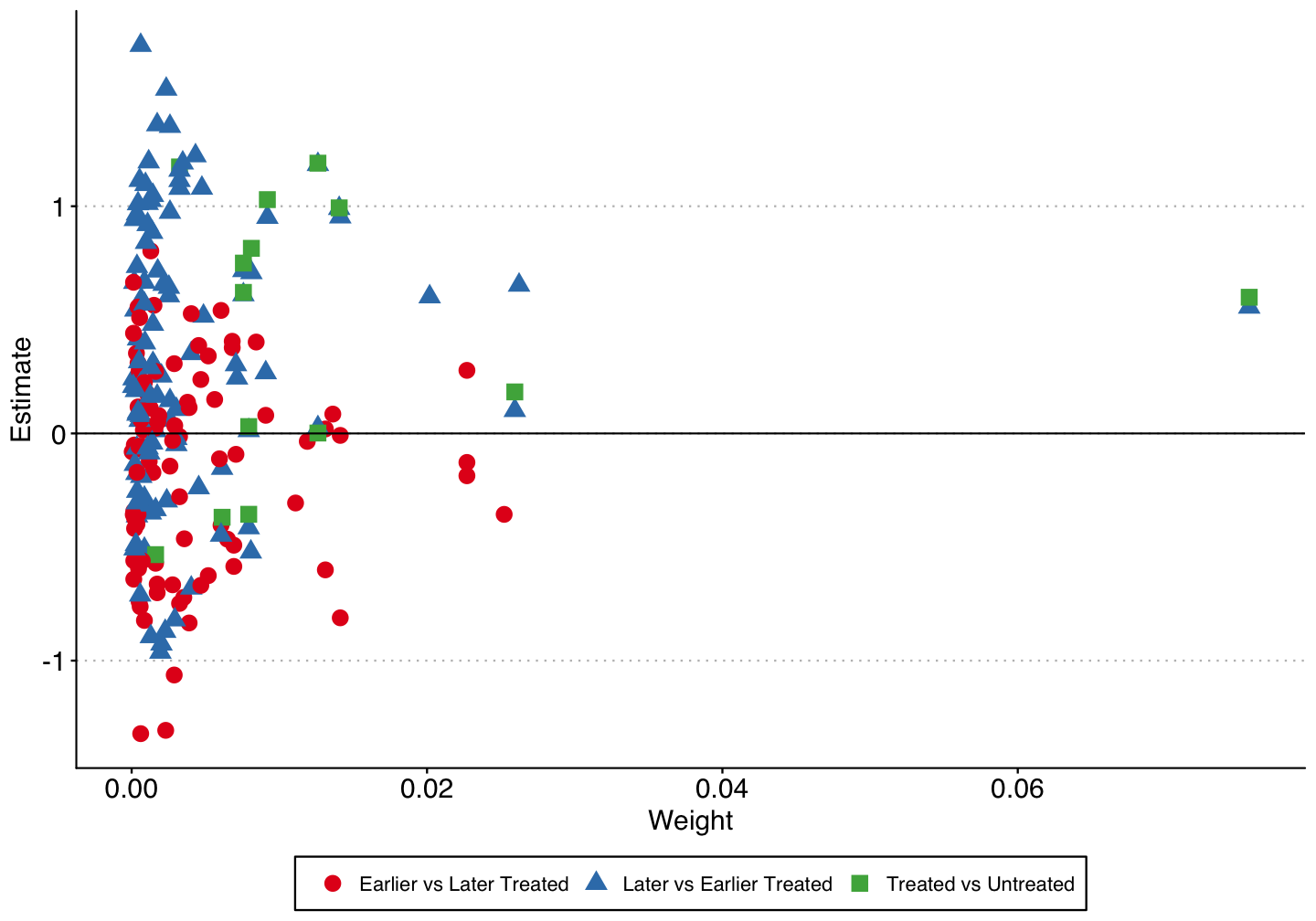
Bacon-Goodman Decomposition
The unweighted average of the 2x2 treatment effects are negative for the earlier vs. later treated (unbiased), while positive for the later vs. earlier treated (biased).
The effect is also positive for the treated vs. untreated units, but there are not many untreated states (i.e. states without medical cannabis laws).
| Type | Average Estimate | Number of 2x2 Comparisons | Total Weight |
|---|---|---|---|
| Earlier vs Later Treated | -0.16 | 91 | 0.38 |
| Later vs Earlier Treated | 0.32 | 105 | 0.42 |
| Treated vs Untreated | 0.44 | 14 | 0.20 |
Callaway & Sant'Anna
Abraham & Sun
- Skip for now - without covariates it's the same as Callaway & Sant'Anna
Cengiz et al.
- First, we can plot the state-specific DiD estimates, separated by adoption period:
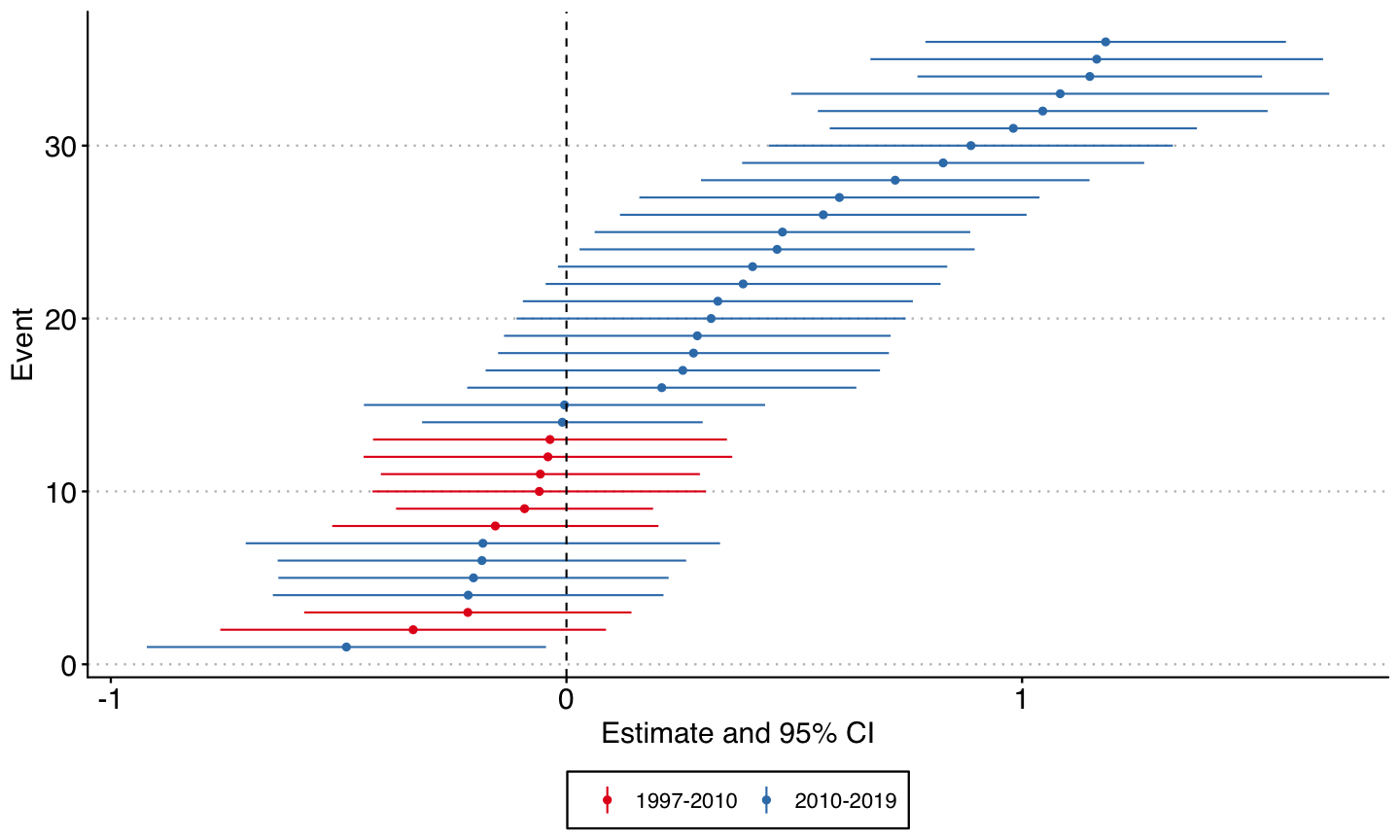
Cengiz et al.
Takeaways
DiDs are a powerful tool and we are going to keep using them.
But we should make sure we understand what we're doing! DiD is a comparison of means and at a minimum we should know which means we're comparing.
Multiple new methods have been proposed, all of which ensure that you aren't using prior treated units as controls.
You should probably tailor your selection of method to your data structure: they use and discard different amount of control units and depending on your setting this might matter.
Unclear what's going on with MMLs and opioid mortality rates, but very unlikely that the results in the first published paper is robust.